This is “Digital mathematics research”
Since: 7/2/03 6:16:40 AM JMT
|
For HomePage “About me.” |
||
|
For Title Page. |
||
|
For OpenLaboratory entrance |
||
|
For BBS. |
||
|
For Mathematics. |
||
|
Contact with |
|
研究室6 “離散数学” <Room 6 Digital mathematics >
離散数学研究室です。 現在準備中。
雑談
索引
e イプシロンの導入による連続関数の離散関数化
(索引)
e イプシロンの導入による連続関数の離散関数化
at: 10/10/03 7:50:10 PM JMT 近藤敏郎
連続数体系における関数に対して、イプシロン(微小な数、とここでは定義付ける。)という概念を導入することで、イプシロンを1とみなす離散数体系(ほぼ、整数体系という概念と同じとみなす)への変換を行なうことは可能であろう。
又、精度(スケールでも良し、)という概念を、導入することで、そのスケールにおける基準値を1とする(具体的には、数体系上の全ての数を、スケールの基準値で割るという操作になるだろう。)離散数体系[1] と扱うことも可能であろう。
以下は、おまけになってしまっている。
f(x)/e ->
Dight f(x)
->: 変換と定義付ける。
除外という、操作についての賛同あり。
つまりは、
fa(x)=fb(x)
O( fa(x) ) = O( fb(x) )
実計算でなければ、この除外と、除外の解除の意味合いはないかも知れない。…
ゼロの意味合いと、1の意味合い。(加えて、掛け算体系で、行なわれている代数的操作に対して、1と0の間の数の、呪いの意味合い? )
メモ、かなりシリアスな研究、アイデアとなってしまったが…、共同研修者ありである。 なのれよな。
代数の相対性[2] についてのひらめきのメモである。 近所の子供だな、これは…、 どこぞの教諭の介入までは、数学のページはもっていたのに…
(e イプシロンの導入による連続関数の離散関数化)
「イプシロンの導入による数体系の自然数体系化」、
「イプシロンの導入による連続関数の離散関数化」、からの発展
12/1/2004 5:40:59 PM JMT 近藤敏郎
ほぼタイトルのままである。
ある数列を考えた場合、最小の数、又は、約数可能な、最小の数というものが考えられる。
例えば、
0.1, 0.04, 0.74,0.0019
以上の4つの数を考えた場合、
最小の数を基準として、自然数化する。
1000, 400, 7400, 19
という数字が、数列に対してのスケールの応用、具体的には1000をかける操作によって、作り出される。
これらの数
警察並びに、チンピラ高校生(地元では有名な、「神戸臭い」・「NHKドラマ臭い」ヤツ)の妨害で中断
又、ファンと証する連中の妨害が会ったことを指摘しておく。「女のほうを捕まえたから」、云々と「中国マフィア」のような「勝ったから、劣情」を繰り広げている、
(おそらくはかたぎの類で、「暴力団だ! 詐欺をあちこちのコンビニ・スーパー、住宅街で繰り広げている何故かそこにいるサラリーマンもどきであろう。」)の妨害による。
追加報:韓国系暴力団の妨害、である。これは、追加で。おそらくは、広島上陸組みであろう。
「とりけせ」、「屈辱だ!」、などと、『岩内警察署』のようなセリフを吐いていたことを指摘しよう。
(「イプシロンの導入による数体系の自然数体系化」)
(雑談)
論文
索引
(索引)
離散関数による、カオス関数グラフの解析
「整数論における豆拾い」のグラフに対する効果
Since: 10/16/2004 8:15:01 PM JMT 近藤敏郎
F(x)=sin(x)
前提として サイン関数を母体として考える。理由としては、無限次元関数[3]であるから、である。カオスなどの関数を考えた場合には、正規系により表記された一般の関数よりも、漸化式、或いは、コンピュータプログラム言語などの新規数学言語[4] により表記された関数が、多いといえるだろう。これは、N次関数・無限時間数という性質に近い、性質をもっていることを意味しているといえる。
いか 、妨害により省略。おそらくは、落ち着ける状態になってから、再記することが、可能だと思う。
まとめ、
サイン関数に対して、種変数の一定の値ごとにサンプリングを行うように値をとり、グラフ化すると、以下のようなグラフが現れてくる。
かなり面白い性質のグラフだと、思うが、どうだろうか?
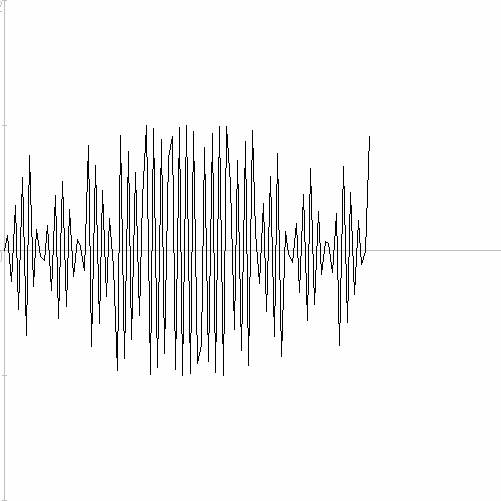
SET WINDOW -10, 1360, -2,2
DRAW axes
FOR i=0 TO 100
LET x=MOD(i*47.0,360.0)
LET v=SIN(x)
PLOT LINES: i*10, v;
NEXT I
END
P.S.
一部の大学の、お馴染みの妨害活動があったことを明記しておく。
ちなみに、例の仏文学者、であるが、どこの大学だろうか? ひとことでは言えないような気がするのだが… ハンバーガーの方だろうか?
北大関連の情報があったら、一報欲しいところである。STVなるものも、存在しているのだし。
掲示板、またはメールにて気軽にどうぞ。一部のマークと妨害は、あいも変わらず続いてはいるのだが。
(離散関数による、カオス関数グラフの解析)
(論文)
update: 10/10/03 8:02:24 PM JMT
update: 10/16/2004 8:23:37 PM JMT
(End of contents.)