This is 幾何学 <Geometry>
|
<for “Title Page”> |
|||
|
<for openLaboratory “theGon”> |
|||
|
<for Home page “About me?”> |
|||
|
<for BBS.> |
|||
|
|
|
||
|
<for Mathematics research room> |
|||
|
|
Contact with |
|
|
|
|
|
||
掲載論文募集中! 掲示板又はメールにて。
幾何学 <Geometry>
![]()
索引
論文
アーカイブ
(索引)
![]()
論文
円周上・球上の点に対する見渡し距離
無限幾何学、極限幾何学
三角形の関係 以下メモのまま 近藤敏郎
2辺端が作る長さ(辺、残りの1辺の長さ)と、その2辺端が作る直線に対する垂線の長さに関する関係 近藤敏郎
ねじれた円錐曲線
(論文)
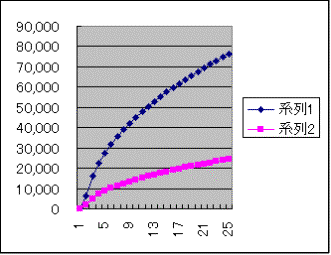
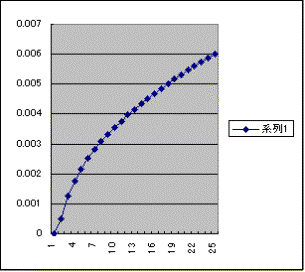
円周上・球上の点に対する見渡し距離
at: 10/20/03 9:52:29 PM JMT 近藤敏郎
|
見当、教育が必要 |
|
|
m |
m |
rad |
|
|
|
|
|
|
|
|
|
|
|
|
|
10000000000 |
10,012,705,469 |
787.5624 |
3,187,143,138 |
|
|
|
|
|
|
|
|
|
|
|
1000000000 |
1,012,633,734 |
79.65002 |
322,331,329 |
|
|
|
|
|
|
|
|
|
|
|
100000000 |
111,994,232 |
8.809052 |
35,648,871 |
|
|
|
|
|
|
|
カタストロフィ点を持つ |
|
|
10000000 |
18,822,083 |
1.480475 |
5991255.026 |
|
|
|
|
|
|
|
|
twilight
を持つ関数 |
|
|
1000000 |
5,140,728 |
0.404351 |
1636344.409 |
|
|
|||||
|
平行線の問題と、ピタゴラスの定理と三角形の問題 |
100000 |
1,597,720 |
0.125671 |
508569.952 |
|
||||||||
|
|
|
|
|
10000 |
504,352 |
0.03967 |
160540.1836 |
|
|||||
|
|
Km |
m |
|
1000 |
159,462 |
0.012543 |
50758.28172 |
|
|||||
|
r |
12713.54 |
12,713,540 |
|
0 |
0 |
0 |
0 |
|
|||||
|
|
|
39,940,764 |
|
1.68 |
6,536 |
0.000514 |
2080.429614 |
|
|||||
|
|
|
|
|
10 |
15,946 |
0.001254 |
5075.729362 |
|
|||||
|
|
l=sqr(h^2+2rh) |
|
20 |
22,551 |
0.001774 |
7178.166714 |
|
||||||
|
|
|
|
|
30 |
27,619 |
0.002172 |
8791.424598 |
|
|||||
|
|
|
|
|
40 |
31,892 |
0.002508 |
10151.46471 |
|
|||||
|
|
|
|
|
50 |
35,656 |
0.002805 |
11349.68482 |
|
|||||
|
|
|
|
|
60 |
39,059 |
0.003072 |
12432.95923 |
|
|||||
|
|
|
|
|
70 |
42,189 |
0.003318 |
13429.13346 |
|
|||||
|
|
|
|
|
80 |
45,102 |
0.003548 |
14356.35037 |
|
|||||
|
|
|
|
|
90 |
47,838 |
0.003763 |
15227.21204 |
|
|||||
|
|
|
|
|
100 |
50,425 |
0.003966 |
16050.89398 |
|
|||||
|
|
|
|
|
110 |
52,887 |
0.00416 |
16834.32293 |
|
|||||
|
|
|
|
|
120 |
55,238 |
0.004345 |
17582.88031 |
|
|||||
|
|
|
|
|
130 |
57,494 |
0.004522 |
18300.84566 |
|
|||||
|
|
|
|
|
140 |
59,664 |
0.004693 |
18991.68881 |
|
|||||
|
|
|
|
|
150 |
61,758 |
0.004858 |
19658.26941 |
|
|||||
|
|
|
|
|
160 |
63,784 |
0.005017 |
20302.97733 |
|
|||||
|
|
|
|
|
170 |
65,747 |
0.005171 |
20927.83413 |
|
|||||
|
|
|
|
|
180 |
67,653 |
0.005321 |
21534.56789 |
|
|||||
|
|
|
|
|
190 |
69,507 |
0.005467 |
22124.66966 |
|
|||||
|
|
|
|
|
200 |
71,312 |
0.005609 |
22699.43659 |
|
|||||
|
|
|
|
|
210 |
73,073 |
0.005748 |
23260.00548 |
|
|||||
|
|
|
|
|
220 |
74,793 |
0.005883 |
23807.3793 |
|
|||||
|
|
|
|
|
230 |
76,474 |
0.006015 |
24342.44818 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||
以上、ほぼメモのまま。
恐らくは、構文エラーが出ると思いますが、気にしないでください。特に問題はない筈です。
(円周上・球上の点に対する見渡し距離)
無限幾何学、極限幾何学
7/10/03
9:58:50 AM 近藤敏郎
9:56
7/10/03
連絡先 tkondo001@livedoor.com
無限、幾何学(着眼点)、極限幾何学
ある点と、X軸上の点に対して伸ばした、直線の極限は?
又、X軸ではなくて、任意の直線上の点では?
以上、原アイデアのまま。 他人の発案についてのメモである。
ない場合には、こちらで、研究を進める。キチンと、掲示版あるいはメールにて連絡すること。
テーゼ:X軸上の点に降ろした直線の角度は、X軸と平行にまでならない(あるいは、平行となるのが極限である。)
(この、極限という用語が、キーポイントである。)
(無限幾何学、極限幾何学)
三角形の重心位置について
7/3/03 6:20:20 PM JMT 近藤敏郎
カオス(フラクタクル)的手法による、三角形の重心位置計算手法を発見したので、報告します。
手法は、以下のとおり
各辺の中点を求める
各辺の中点を繋ぐ三角形を考える
以上の、手法を、点が収束するまで、繰り返す。
プログラムは、次に
(仮称)十進ベーシックを使用しています。
OPTION BASE 0
REM 重心計算のアルゴリズム
REM オリジナルアイデアは、プログラム製作途中の口出し、推薦済み(家族が反対か?)
REM 03/03/Jul 18:15 JMT
REM program by Tosiro.Kondo
REM
DIM x(4),y(4)
DIM gx(4),gy(4)
LET pre=1.0
REM precision condition
RANDOMIZE
FOR i=0 TO 2
LET x(i)=RND*100
LET y(i)=RND*100
NEXT i
100
SET WINDOW -10,100,-10,100
DRAW axes
FOR i=0 TO 2
PLOT POINTS :x(i),y(i)
PLOT LINES :x(i),y(i);
NEXT i
PLOT LINES :x(0),y(0)
FOR i=0 TO 1
LET gx(i)=(x(i)+x(1+i))/2
LET gy(i)=(y(i)+y(1+i))/2
NEXT i
LET gx(i)=(x(0)+x(2))/2
LET gy(i)=(y(0)+y(2))/2
SET color 2
FOR i=0 TO 2
PLOT POINTS :gx(i),gy(i)
NEXT i
FOR i=0 TO 2
LET x(i)=gx(i)
LET y(i)=gy(i)
NEXT i
REM
LET xsum=0
LET ysum=0
LET xsum=xsum+ABS(x(0)-x(2))
LET
ysum=ysum+ABS(y(0)-y(2))
FOR i=0 TO 1
LET xsum=xsum+ABS(x(i)-x(1+i))
LET ysum=ysum+ABS(y(i)-y(1+i)) NEXT i
IF (xsum < pre) AND (ysum < pre) THEN GOTO 200
GOTO 100
200
PRINT x(0),y(0)
END
以上。
ダウンロード
(三角形の重心位置について)
ねじれた円錐曲線
6/22/03 6:05:14 PM 近藤
ねじれた円錐曲線
○現代美術の数学への応用
円錐の変わりに現代的なオブジェを用いた曲線の探求
○
3Dオブジェクトグラフによる、非円錐曲線の表現
オリジナルメモ
古典的な円錐曲線の理論体系と研究に変わる現代数学、美術の問題。
トポロジカルな側面も多々あり。
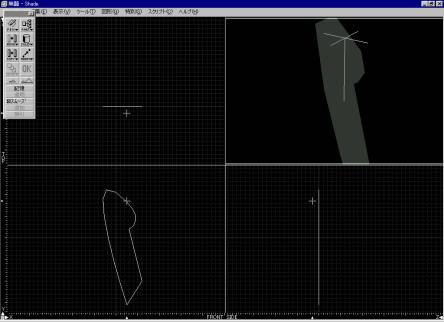
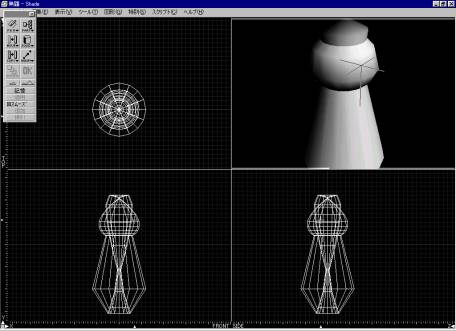
例としていかに、シェード(体験版)で、作った、比較的単純な立体オブジェとそれに対する研究を示す。
|
図 1 回転体の元図形 |
図 2 回転体 |
|
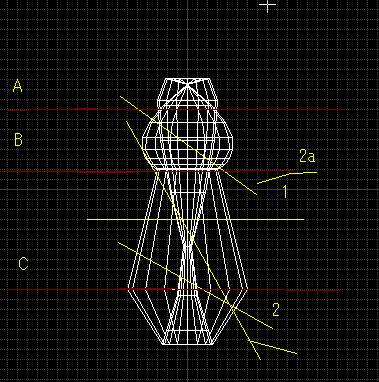
図 3 YX断面拡大図 作業線入り |
かような立体を形成。この立体を円錐の変わりに用いて円錐曲線群を求めてくると Y軸に平行な軸を想定した回転体であるから。 1: 真円に相当 2: 双曲線に相当 3:放物線に相当 4:(開いた)放物線に相当 という所謂円錐曲線群とは、1対1の相関をなくすと云えそうである。 このオブジェに対する、円錐曲線同様の分類分けを行うと 区間A,B,Cとその関連 1.Y軸に垂直な面による切断面(曲線)は、半径の異なる真円いくつかに変換 2. 3. 4. |
|
|
というように、 Y軸上での目盛り位置 回転中心軸との交差位置(Y軸目盛り)と傾斜、(Y軸からのX距離に応じたYの変量) 以上、の要素による、関数の特定は可能である。 これは図形による。 (恐らくは、堀越さんの付加あり。多分に、つまみ食いになっているんだよな。変な若いのは、おなじみ射殺されたい「僕だよ〜ん!」スタイルで出てくるし。その昔は、バカ女だったよな。) |
|
|
以上の、事柄については、オブジェクトを選択する自由さ、から、無限に円錐曲 線同様の研究対象並びに
また、基本図形と、堀越発案[1] [2] の曲線定義要素、から、曲線を分類するのは、困難ではなかろう。系統的に、曲線を分類するのも、恐らくは、そんな困難ではないと考える。
(ねじれた円錐曲線)
2辺端が作る長さ(辺、残りの1辺の長さ)と、その2辺端が作る直線に対する垂線の長さに関する関係 近藤敏郎
6/15/03 12:36:06 AM JMT
ヘロンの公式関連の思索から
共同研究者求む!
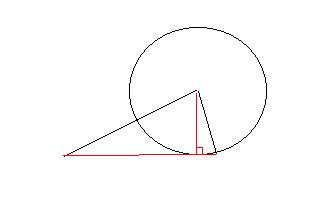
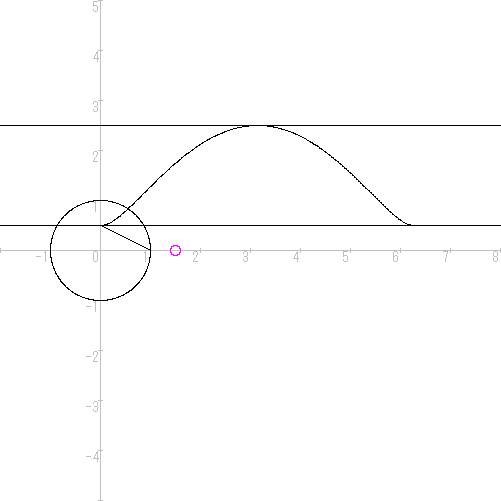
図 4
まで、
6/17/03 6:04:12 PM JMT
数値解析の手法を導入して、この問題を解きたいと思う。先に、問題にあたる疑問の提示並びに、数学のページWANTED掲示板として、共同研究者の募集をあげていたので、既に解けている人間、ならびに理解を深めている人間も多いと思う。
|
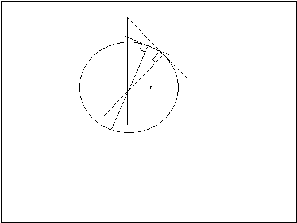
図2を照して欲しい。 円周上を移動する点と任意の点との関係は、図1 のようになる。 |
図 5 |
|
||
|
|
|
|
|
|
ダウンロード
「(仮称)十進ベーシック」による補助プログラム
(2辺端が作る長さ(辺、残りの1辺の長さ)と、その2辺端が作る直線に対する垂線の長さに関する関係 )
3辺と三角形の面積の関係 以下メモのまま 近藤敏郎
4/22/03 1:34:32 AM JMT
14:11 4/10/03
S=Sqrt(s*(s-a)(s-b)(s-c))
ここで
a< b+c
a > abs(b-c)
b < a+c
b > abs(a-c)
c < a+b
c > abs(a-b)
(s-a)(s-b)(s-c)
(s-a)(s^2-s(b+c)+bc)
a < b+c
a >abs(b-c)
->
面積に関して
2辺が決まると3角形の最大面積が決まる
(三角形の関係)
( 三角形の関係)
![]()
アーカイブ
(アーカイブ)
|
|
プログラム名 |
備考 |
|
|
|
|
|
|
|
|
三角形の重心計算プログラム |
|
|
|
|
|
|
|
Updated: 7/3/03 6:26:32 PM JMT
Updated:
10/20/03 9:56:01 PM JMT
<End of Contents. >