This is ���_�@���w�������S <Research room 4>
|
<for �gTitle
Page�h> |
|
|
<for openLaboratory �gtheGon�h> |
|
|
<for Home page �gAbout me?�h> |
|
|
<for BBS.> |
 Contact with tkondo001@hotmail.com
Contact with tkondo001@hotmail.com
���_ <Numeric>
��ʓI�Ȑ��̐��藧���ɂ��Ă̌����ł��B
<General research for numeric. >
������A�l�I�Ȏ���ɂ��A�����r��Ƃ�����Ԃł��B
<All of these are in progress, sigh. >
�e�[�}
Index
![]()
�f���_�ɂ���
6/26/03 3:51:49 PM JMT�@�ߓ��q�Y
�@�f���Ƃ��̑̌n���ʈ����ɂȂ��Ă���̂́A���͕s�v�c�Ȃ��Ƃł���B���̑̌n����́A���ɐ���Ƃ����T�O�����w�̐��E�ɂ͒���[1]�@���̌n���̂��̂ɂ��Ă̐�ւ��ƁA���̐��̌n�ɂ��Ă̌������A�s�Ȃ��Ă��A�s�v�c�͂Ȃ��Ƃ����ɁA����̐��w������Ɖ]���邩��ł���B
�@
�f���_������
�i�f���_�ɂ��āj
![]()
���̒�`
�@���̒�`�́A������ɂ߂�d���ł���B
�@����̐��w�̏펯����́A�O���t���_�̃|�[���@�A�����グ���_�́������Ƃ������ƂɂȂ�̂�������Ȃ��B
���R���̒�`�́A�q���[�����тɏd�_��`�E�d����`�̋ߑ�̓N�w�ҒB�̋c�_�������A���̊T�O�Ɛ�����Ƃ����s�ׂ͖��l�i���̏ꍇ�͒m�������������݁j�ɔ�������펯�ł���A�Ƃ����ߒ��Ɋ�Â��Ă���ƌ�����B
���́A���R���Ƃ������c�́A���̐��I�����i�P��������Ƃ������j����ɂ���Čn�����������邱�Ƃ��o���鐔�̂��Ƃł���B[2]
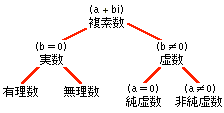
�@���炭�́A�Ƃ����ߒ��Ɠƒf�Ɋ�Â��āA���̑̌n�ɂ��āA�ȉ��̕��ނƍ\�����Ƃ�B�i�^��E�c�_���}�ł���B�j
���R��
����
����
����
������
����
���w����ł̕\�L��
�}�i���R���j���i�����j���i�����j���i�������j���i�������A�����L���j
�Ƃ����A�L�ڃX�^�C���ɂȂ邾�낤�B
����́A�ʐl�̈ӌ��ł��邪�A�u���Ƃ́A�������ł���ׂ��Ƃ����N�̎咣��W�J����Ƃ��̂��炢�Ƃ����������Ő������������w�W�ł����\�L�ł��Ȃ��ł͂Ȃ���?�@�v�A���̘_���𗠕Ԃ��Đ��̒�`�ɂ��čl�@�Ƃ��������ɉ��������̂ɂ����ꍇ�A�u��̓I�Ȑ��i�Ⴆ�O�ɂ܂��c�_��P�Ƃ������ɂ��Ă̐����Ȓ�`�i�Z���I�ȂƂ����Ă��������j�j�Ƃ͈قȂ鈵�����ɂ��A���m�T�V�Ƃ������̊T�O���o�Ă���B�v����́A��ςɖʔ����A�C�f�A�ŁA���ɂ��Ă̖{���I�E�N�w�I�Ȑ��@�̈�Ƃ݂Ă��ǂ��A���낤�Ƃ����ӌ��ɂȂ��Ă���B�i�Ȃ�ƂȂ��A�T���o�ި�Ɋ��ӂ������Ȃ��Ă���BThanks for somebody.�j
�ȏ�ɂ��ẮA�ȉ��̍��ڂ��Q�Ƃ̂���
�⑫�F���тɁA���p
���@�i���w�j
����
���̌��𐔂��邱�Ƃ��玩�R���i�������j�����܂ꂽ�B���������R���̏W���ł͉��@�Ə�@�����\�łȂ����߁C���@���\�ɂ��邽�߂O�ƕ��̐��������������Đ��������܂�C����ɏ��@���\�ɂ��邽�ߗL�����i�����Ə����̂Q�\��������j���l����ꂽ�B����ɐ��̘A�������l�����Ė������������Ď����֊g������C�܂��㐔����������ʂɉ�����悤�ɂ��邽�ߋ����������f�����l����ꂽ�B�ӂ����Ƃ������̕��f���܂ł͈̔͂��������C���������Ɋg�������l�����Ȃǂ�����B���l��
���֘A����
���S��|�L���@|����
�}�C�y�f�B�A for Win������������f�W�^���u�}��
�l�����@
������
���f�����g���������̂Ŏl�̒P�ʂP�Ci�Cj�Ck�������Ca�Cb�Cc�Cd�������Ƃ���a�{bi�{cj�{dk�̌`�ŕ\�����B��̎l�����̉����͕��f���̏ꍇ�Ɠ��l�����ςɂ��Ă�i2��j2��k2���|�P�Cij���|ji��k�Cjk���|kj��i�Cki���|ik��j�ƂȂ�B����ɂ��l�����͏�@�̌����@�����������ׂĂ̑㐔�@���i�����@���C���z�@���j�����藧���C���̏W���͔���̂ƂȂ�B1840�N����W.R.�n�~���g���������B�w�C�����w���ɉ��p�����B����
���֘A����
�㐔�w
�}�C�y�f�B�A for Win������������f�W�^���u�}��
���@�����@Number
���̂̌��𐔂�����A�����A�召��ʂ̂悤�Ȃ��̂��������߂���܂��͋L���B���w�̗��j�ƂƂ��ɁA���͈Ӗ��̖L�����ƕ��G�����܂��Ă����B
�L����
�����Ƃ��ȒP�Ȑ���1, 2, 3, ... �̂悤�Ȏ��R���ł���B���R���́A���̐������邢�͐��̗L�������Ƃ������B���R���Ǝ��R���ɕ��̋L�����������́A������[��(0)�����킹�����̂������ł���B���R���S���̏W���́A�a�ƐςɊւ��ĂƂ��Ă���B�܂�A2�̎��R���̘a�A����ѐς͂܂����R���ł���B2�̎��R���̏�(����Z�̌���)�͎��R���Ƃ͂�����Ȃ��̂ŁA�C�ӂ�2�̎��R���̏�����ɂ��邽�߂ɂ́A���̕������l����K�v������B�����ŁA���R��n�́A���� n/1 �Ɠ������̂��Ƃ���B����ɁA2�̐��̕����̍��͐��̕����Ƃ͂�����Ȃ��̂ŁA���̕���(���̐������܂�)��0���l���Ă������ق����֗��ł���B������ѕ��̐����ƕ�����0�����킹�āA�L�����Ƃ����B
2�̗L�����̘a�A���A�ρA����їL������0�łȂ��L�����Ŋ����������L�����ł���B���ׂĂ̗L�����͏z�����A�܂肠��ʂ����낪�L���̐�����Ȃ�u���b�N�̂��肩�����ƂȂ鏬���ł���킳���B�t�ɏz�����͗L����������킷�B���Ƃ��A617/50 = 12.34000... �� 2317/990
= 2.34040... �Ȃǂł���B�ŏ��̗�͗L�������Ƃ������A0�̂��肩�������͂Ԃ��āA12.34�Ə����̂��ӂ��ł���B��2�̗�́A4��0����Ȃ�u���b�N�����肩�������z�����ł��邱�Ƃ����߂����߂�
![]()
�Ƃ���킷�B
������
�w�̔��B�ƂƂ��ɁA����ɕʎ�̐����K�v�ɂȂ����B���Ƃ��Β��p�ӎO�p�`��2�ӂ̒�����1�̂Ƃ��A�Εӂ̒����͗L�����ł���킷���Ƃ͂ł��Ȃ��B�܂��A�~�������L�����ł͂Ȃ��B�������Ė��������Ƃ肢��邱�Ƃ��K�v�ɂȂ��Ă���B�����ɓW�J�����Ƃ��ɗL�������ɂ��z�����ɂ��Ȃ�Ȃ���A���̐��͖������ł���B���Ƃ���
¸ = 1.4142135623... �� p = 3.1415926535... �͖������ŁA�����ɓW�J����Ɩ����ɂÂ��A�z�����ł��Ȃ��B�L�����Ɩ����������킹�Ď����Ƃ�ԁB
���f��
�����̕�����0�܂��͐��̐��ł���B���������āA������
x2 = -1 �͎����͈̔͂ł͉����Ȃ��B���̂悤�ȕ������ɂ������������悤�Ƃ���Ȃ�A�V���������������܂Ȃ���Ȃ�Ȃ��Bi = · ���A���̕������̉�������킷�V�������Ƃ���Ba + bi (a�Ab�͎���)�̌`�̐������f���Ƃ����A���f���S���̏W���f���̂Ƃ����Bb��0�łȂ����f���������Ƃ����Aa��0��b��0�łȂ����f�����������Ƃ����Bb��0�ł���A���̕��f���͎����ł���B���f���͓d�C��H�̗��_���͂��߁A�����w�Ȃǎ��R�Ȋw�̕���łȂ��Ă͂Ȃ�Ȃ����̂ɂȂ��Ă���B���܂��܂Ȏ�ނ̐��́A���̕\�ɂ��߂��悤�ȊW�ɂȂ��Ă���B
1779�N�Ƀh�C�c�̐��w���K�E�X�́A
xn + a1xn - 1 + ... + an - 1x + an = 0(a1, a2,
..., an �͕��f��)
�̌`��n���̑㐔�������͏��Ȃ��Ƃ�1�̕��f�������������Ƃ��ؖ�����(�� �������_)�B
�����͒�����̓_�Ƃ��Ă���킳��邪�A���f���͕��ʂ̓_�ɑΉ������邱�Ƃ��ł���B���f�� a + bi �� xy ���ʏ�Ŋw�I�ɂ���킷���߂ɁAx��������a�̎��Ƃ��Ă������Ay����������bi�̎��Ƃ��Ă�������B���f��
a + bi �͍��W (a, b) �����_P�ɑΉ�����B���_O����_P�ɂ������x�N�g���ɂ���ĕ��f�� a + bi �Ƃ���킷�ƕ֗��ł���B��1�ی��ɂ��镡�f�� a + bi �� -1 ��������ƁA�x�N�g��OP��180����]���āA�_P�͑�3�ی��Ɉڂ�B�����v����90���̉�]�́A���f����i�������邱�ƂɑΉ�����B
���j��A���ɑ��ĂƂ��ɋ����[���l���������߂����̂��A����w�ł���B����́A���ɂ��Ă̏ے��I�Ӗ����肪����ɁA�����ɂ������ꂽ�_�����݂Ƃ낤�Ƃ��鎎�݂ł���B���Ƃɂ��Ă���̂́A�M���V�A�̓N�w�҂Ő��w�҂ł����s�^�S���X�́A�����͐��ł���A���܂��܂Ȋw�I�p�^�[������Ȃ��Ă���Ƃ������`�ł���B[3]
�i�u���̒�`�v�̏I���j
�������ɂ���
�������̍����ƁA�f���̂悤�Ȗ����������݂���\���ɂ���
��ꖳ�����ɂ���
�i�������ɂ��āj
�����Ƌ����̊�
�����Ƃ́A�����ɑ���Η��T�O�ł���Ƃ�����B���R���A�O�A�����A���i�ϐ����͖��m���ł���j�A�����ƁA���ɑ��錤���ƊT�O�́A�i��ł������A�����̔����ɂ���āA���A�����Ƃ����T�O���������ꂽ�ƌ�����B
�@�����_�ɉ�����A�����̒�`�́A�u�����Ŗ������v�A�Ƃ������ƂɂȂ邾�낤�B
�@�����łȂ��Ƃ���Ȃ�A�����̒�`�Ƃ������̂��A�ʂɑ��݂���Ƃ������ƂɂȂ�B���A����͎����Ƌ����Ƃ̊Ԃɕʂ̐��̊T�O�����݂���Ƃ������_�����A�c�_�ւƑ����B
�@�����Ƌ����̊ԂɁA�i��ɂ���āA�����ӂ̗��_�W�J���ȁA�Ɛ��������������ȋC�����邪�c�c�j�A�ʂ̐��̊T�O�����݂��邩�Ƃ����^��ɗ�������B
�@�����_�ł́A���̏��_���́A�u�����Ƌ����̊Ԃɕʂ̐��̊T�O�����݂��邩?�@�܂��A�����邩?�v�Ƃ����^��̒ŏI���B
�i�����Ƌ����̊ԁj
�����Ɗ <Odd & Even>
�����Ƃ͂Q�Ŋ����鐔�i�Q�̔{���j�A��Ƃ͂Q�Ŋ����Ȃ����i�Q�̔{���Ŗ������j�B�Ƃ����̂��A��E�����̒�`�ł���B
���́A�Q���������ʁH�@�Ƃ������Ƃ��v�����Ă��܂����B
���̍l����W�J���Ă����Ƃ��̗l�ɂȂ����B
�Q�ɑ���
� �Q�̔�{��
���� �Q�̔{��
�R�ɑ��Ċ �R�̊�J�e�S���[�P �R�̔{���{�P
�R�̊�J�e�S���[�Q �R�̔{���{�Q
���� �R�̔{��
�S�ɑ��Ċ �S�̊�J�e�S���[�@�P
�S�̊�J�e�S���[�@�Q
�S�̊�J�e�S���[�@�R
���� �S�̔{��
�ȉ����l��
N�̊�@�J�e�S���[�@�P
�c�c
N�̊�@�J�e�S���[�@�in-1�j
�ȏ�A�ł���B
�����ł���B���A�����̃������ǂ߂Ȃ���ԂɂȂ��Ă��܂����B
�i�u��Ƌ����v�̏I���j
�����L�����iT�̖����j
�������̕����\�L�ɂ���āA�V�K�̐���\�L�ł���B �i�������̃A�C�f�A�B�����o�Ă����ƁA���܂����܂߂ċL�ڂ���B�j
�L�����ɂȂ�ꍇ��
�������ɂȂ�ꍇ�����݂����邾�낤�B�iT�@�⑫�j
�ȏ�̕\�L�ɂ�閳�������A�����L�����i�������̔��e�ɑ��݂���A�L�����I�Ȑ��j�ƒ�`�Â���i���ł���j�B
���A���l�ɁA
���ɂȂ閳��������̌n�������I�Ȑ�����[4] �ɂ���āA�n���I�ɔ��������邱�Ƃ��o����B�@�i�������_�Q�Ƃ̂��Ɓj
�F���l�̐��w
��ʓI�Ȑ����A��ɂ��̌n���̒��ŁA��O�̐�������傫���Ƃ����̂́A��X�n���l�ށi���ʂƂ͌���Ȃ��̂ł��邪?�@�j�̊��K�ł���B
�@���̌n�����A�Ⴆ�Ώ�Z�ł��A���̑̌n�ɂ͕ω��͖����̂ł�?�@���炭�́A�|���Z�̑��삪�ʗp���Ȃ��Ȃ�A���̔��_�����锤�ł��邪�A�قȂ鉉�Z��Ⴆ�ɏo�����A�|���Z�̕ς��ɗp���邱�Ƃ͉\���낤���A���̗l�Ȑ��w�̑̌n�����݂����邾�낤�A�Ƃ����A�^�₪�A���ɂP�T�N�ȏ�O�̂P�X�X�O�N��ɓ����߂������B
�@��r�I�|�s�����[�ȃA�C�f�A�ɂȂ��Ă����\��������̂ŁA���̐��̌n�Q�i�F���l���p����A�F���l���p���Ă��邩������Ȃ��A�Ƃ����j�ɂ��Ă̌������i��ł��邩���m��Ȃ��B�m�F�A�o����j���[�X�̗ނ��ɂ͐ڂ��Ă��Ȃ��̂ŕs���ł��邪�i�m���́A�ǂ�ǂ�ƂO�ɋ߂Â��Ă��锤�ł͂��邪�c�c�@J�j
�@���A���������A���w�����ΐ����K���̂́A�����̂��Ƃ������낤���H
�@�Ȃ�ƂȂ��̋^��ł���B
history:
updated: 6/26/03 3:33:53 PM JMT
<End of contents. >