This is 数理モデル1 <Mathematical model 1st of e-motor. >
タイトル <for Title. >
公開研究所 <for OpenLaboratory >
工学研究室 <For Engineering Entrance>
モーター研究室 <Motor res-room Entrance. >
数理モデル1 <Mathematical model 1st of e-motor. >
対象とするのは、基本的には、2極モーターといわれている種類のもので、
<In this room, Motor mean generally bi-polar (?) motor. >
ある人からの指摘により、サイン(三角、と言うよりも循環)関数をモデルに導入したらどうだ? という指摘があったので、ここでは、2つの基本的な2つのモデルによる、モーターのモデル(運動と仕組み)の説明であるモデルを掲載します。
<Someone give advice, “Use sin function (rather recurring function. See Math. pages ) for model.” Then here are 2 kind basic motor mode, movement and mechanism explanation. >
モデル1_0 <Model 1_0>
基本的なモデルの説明。
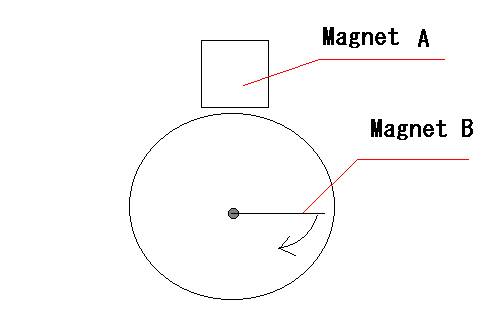
図0
図1に示したのが、基本モデルの模式図です。
磁極は、2つで、時局の制御は、このモデル中では取り上げない仕組みによって行われるものとします。
初期位置は、このモデル中では取り上げない仕組みによって、磁石Aの左右どちらかで、近い位置に停止しているものとします。
ローター(回転子)の磁極はどちらでも良いのですが、N極又はS極で固定です。また、二つの磁極は、同じ強さだとします。
回転方向は、右回りです。
磁力の強さを :X
角位置(真上を0と置き、時計回りに角度を振った場合の、角)を :t
時間を :m
回転モーメント(固定)を :M
軸中心から、回転子磁石の中心位置までの長さを :l
とおいた場合
磁石同士の間に働く力は
f=Mm/d^2
という万有引力の方程式同様、場の力の方程式で現されることになります。
又、
時間 :m (計測時間)に係わらず
角位置 :t により一意に決まる関数で現すことが出来ます。
ここで、円周上のある点からの角による距離の変化は
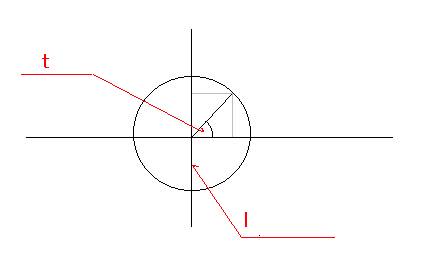
図 1
座標(x 、y)で現される点 (1 , 0) (本当は、どうでも良く、x か y の値のどちらが1で別の点が0である点であれば良いのだが。)からの、円周上点
(x、y) = (l*cos(t) 、 l*sin(t))
と(1、0)からの距離 D
=sqr( (1−l*cos(t))^2
+ (-l*sin(t))^2)
によって現されることになります。
よって、
f=Mm/d^2 から
f=X^2/ (1- l*cos(t))^2
+(-l*sin(t)^2)
が、このモデルに於ける基本的な力の方程式ということになります。
又、向きを考慮に入れると、
注 <Annotations:>
e-motor : electric motor.
<End of Contents. >