This is �������R <Room 3>
�^�C�g���y�[�W <for Title.>

���J�������@"theGon" <for openLaboratory �gtheGon�h. >
���w������ <for Mathematics �gEntrance�h. >
�ʔ����� <Function. >
<Sorry, not translated, yet. >
index
 ���̃y�[�W�ŗp����p��ƍl�����ɂ��Ă̐���
���̃y�[�W�ŗp����p��ƍl�����ɂ��Ă̐���
�Q�����\�L�ɂ��@v=��^2/v�@���A�A���A��ϐ��w�̕ω����͔C��
�H�w�I��[1]�Q ���݁A�������ł���B
���ƃO���t�ɂ��Ă̌������s���Ă��܂��B
<Study of function and graph. >
2*n�����ɂ���
�Q�����̍����ɂ���
��W��
<Wanted.�@>
���̎��A�O���t�ɂ��ẮA���ݕ�W���ł��B
<Collecting function and Graphs. >
���̎��T�@Index
�f�J���g�O���t�iX,�@Y�A�c,�@Z�j < Descartes functions.>
�Q�����O���t <Plane functions >
�P���P���� <one unknown linear functions (equation). >
1���Q���� <one unknown quadratic function (equation). >
�R�����O���t <3-d Graph. >
n�����O���t <n-D graph. >
��f�J���g�O���t
�}��ϐ��\�� <Parametered functions>
�}��ϐ��P�� <Parameter one unknown linear function>
�}��ϐ�N�� <Parameter N unknown function. >
���e
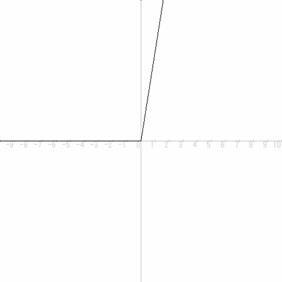
����Ax+B ����
A:�萔�A��ʓI�ɂ͎����͈͓̔�
B:�萔�A��ʓI�ɂ͎����͈͓̔�
�����̃O���t �^�C�g���ɂȂ��Ă���͈̂�ʌn�Ƃ�����\�L�B
������肷���̗v�f�i�p�����[�^�[�j������
(End of paragraph)
�I���I�t��
7/17/03 11:34:36 PM�@�i�l�s�@�ߓ��q�Y
�@�o�͂��O���͂P�ɂȂ���B
�@���݁E��W�Ȃ�тɌ������B
�@�`�h�����ɗp����\��B�@�p�Y�����̒�`�ɗp����A�A���������̕��i�Ƃ���\��ł���B
�i�I���E�I�t���j
����Ax^2+Bx+C �Q���Ȑ�
A�F�萔�A��ʓI�ɂ͎����͈̔�
B�F�萔�A��ʓI�ɂ͎����͈̔�
C�F�萔�A��ʓI�ɂ͎����͈̔�
�Q���Ȑ��̃O���t �^�C�g���ɂȂ��Ă���͈̂�ʌn�Ƃ�����\�L�B
������肷��R�̗v�f�i�p�����[�^�[�j������
(End of paragraph)
y=xx ���ȑΐ����i����j <Self-logarithm function>
�Ǝ����F
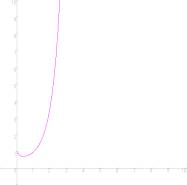
���R�ΐ��̒�@1/e�@���]�ϐ��ŏ��l�̍ۂ̎�ϐ��̒l�ƂȂ�.
�ؖ��́A�L���r���B�⑫���}�B
Wednesday, August 16, 2000 2:23 PM
(End of paragraph)
y=x-x �t���ȑΐ��i����j <Anti-self-logarithm function>
�Ǝ����F
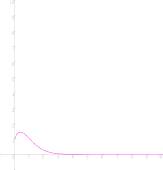
���R�ΐ��̒� 1/e ���@�]�ϐ��̍ő�l�̍ۂ̎�ϐ��̒l�ƂȂ�B
�ؖ��́A�L���r���B�⑫���}�B
Wednesday, August 16, 2000 2:23 PM
(End of paragraph)
Y=X-1/x �t���ȋt�ΐ��i����j <Unknown,�@but Anti-self-anti-logarithm function. J>
�Ǝ����F XX����̃A�C�f�A�A�C�f�A�ł���B���_�ɂ��Ă��邻���Ȃ̂ŁA���҂ł������ł���B
XX����Ƃ͓���l�A���O���R�炵���̂�[2]�A�c���̂ɂ��Ă����̂ł���B

�t���ȑΐ����̒��Ԃł���B
�i ���l�̊��́A���S���x���݂������ł���B�V��A���́A�����[�����Q�ƂȂ邾�낤�B����������A�����������B
XX��������l�ł���B�͂�����ƁA���O�Ə����g�D[3]�@�𖾂炩�ɂ��A�����Ƃ��̑��̊W�L�������̂ŁB
�v���C�Y�ɂ��ẮA����͍l�����܂��B�@���S�ɂȂ��Ă��܂����B��قǂ��̃p���O���t�͍폜���܂��̂ŗ����̒��B
�j
12/28/2000 8:38:46 PM
(End of paragraph)
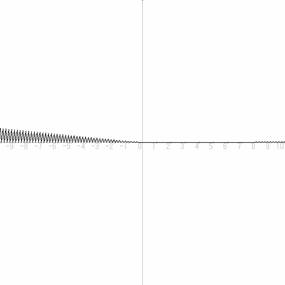
�Q�����\�L�ɂ��@v=��^2/v�@���A�A���A��ϐ��w�̕ω����͔C��
�@�Q�����\�L�ɂ����̕ω��̓x�����A���G���ƁA�o�͂̑z���t���ɂ����́A�T���v���Ƃ��Ăł����グ�����ł͂���B
�ȉ��́A�v���O����
�\�i�x�[�V�b�N�ɂ��A�v���O����
SET WINDOW -10,10,-10000,10000
DRAW axes
LET
v=1
FOR i=-1000.01 TO 10000 STEP 0.1
LET v=i^2/v
PLOT LINES: i, v;
NEXT I
�v���O�����́A�ȏ�B
�J�b�g�A���h�y�[�X�g�ŁA�\�i�x�[�V�b�N�̃G�f�B�^�[�ɓ\��t����ƁA���̂܂܁A����\�ł��B
END
|
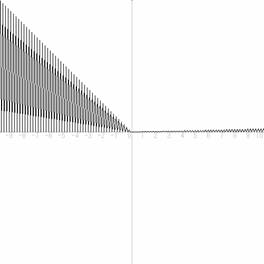
�@�w�̕ω��ʁ@�O�D�P �@�u�̏����l�P�D�O�̏ꍇ�̃O���t
|
�w�̕ω��ʂP�D0, V�̏����l�P�̏ꍇ�̃O���t
|
�w�̕ω��ʂP�D�O �u�̏����l�O�D�P�̏ꍇ�̃O���t
|
|
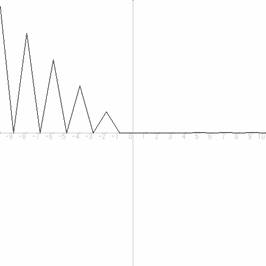
�@�w�̕ω��ʁ@�O�D�P �@�u�̏����l�P�O�D�O�̏ꍇ�̃O���t
|
�@�w�̕ω��ʁ@�O�D�P �@�u�̏����l�P�O�D�O�̏ꍇ�̃O���t
|
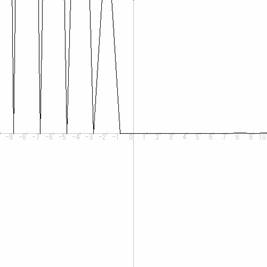
�@�w�̕ω��ʁ@�P�O�D�O �@�u�̏����l�O�D�P�̏ꍇ�̃O���t
|
�����ŁA�ЂƂN�C�Y�A
�@�w�@�̋Ɍ����O�̏ꍇ�́A���̊��̃O���t�́A�ǂ��Ȃ�ł��傤���H�@���́A�z�����t���Ȃ��������̂ŁB J
�o�D�r�D
�@���������ɁA�u���m�̒m�v���w�ԁA�ł����̂������c
������

�O��
�������f�J���g�O���t�ŕ\�L���邱�Ƃ͏o���Ȃ��B�����_�ł̐��w�̏펯�ł́A��ϐ��ɑ��ĕ����̒l�������́A�}��ϐ���p���ĈȊO�ł́A�O���t�����ɕ\���ł��Ȃ�����ł���B[4]
����āA�����ɋL����Ă��闆�����͔}��ϐ��ɂ���Ă���B
�}��ϐ��\�L�̐��w�ɂ��ẮA���������ł��邪�A�}��ϐ��\�L�Ɣ�}��ϐ��\�L���q�����w���삪�����Ă������̂ł͂Ȃ����ƍl����B
!�@x=cos(t)(t/range)(1/a)
!�@y=sin(t)(t/ramge)(1/b)
!�@
! ������
! t :��ϐ��i�}��ϐ��j�@�p�x
! range :�ŏI�p�x
! t/range :������
!�@
1/a :���S���i�G�����j
! 1/b :���S���i�G�����j
!
! t:-inf <-> inf �i�}�C�i�X�������疳���ɂ�����A��ʌ`�ł��邽�߁j
! x^2/a+y^2/b=k*t^2
!
! a :���S���i�G�����j�i�i�t���j�j
! b :���S���i�G�����j�i�i�t���j�j
! k :�������W��
! t :�����ϐ�
!�@����l�̏��߂ŁA���̂܂܂̌`�Ōf�ڂ��邱�Ƃɂ��܂��B
! �����ɂ��Ă̈�ʌ`�ł��B
!
����.BAS�i�\�iBASIC�j �T���v���v���O�����@�_�E�����[�h�i�_�E�����[�h�e�X�g�Łj
(End of paragraph)
���T�[�W�����Q
�ȉ��́@�w�}�C�y�f�B�A for Win��������Г����f�W�^���u�}�Ёx����̈��p
���T�[�W���̐}�`�@
���T�[�W���̂�����
�݂��ɒ��p�����ɐU�������̒P�U�����������ē�����}�B1855�NJ.A.Lissajous�k1822-1880�l���l�āB��̐U���̕����ɒ��p���W���Ƃ��ăO���t��`�����@�̂ق��C�u���b�N�o�[���̐U�q��I�V���O���t���g���ĕ����I�ɕ`�����邱�Ƃ��ł���B��̐U���̐U������ʑ����ɂ���Ă��܂��܂Ȑ}�`��������B
�}�C�y�f�B�A for Win������������f�W�^���u�}��
�i���p�͈ȏ�܂Łj
��{�I�ɂ́A�ȉ��̐����ŗ^������Ȑ����ł���B�c��Ȍ������ʂ��܂��m���Ă���̂ł͂��邪�A���ɗL�v�ł���ׂɁA��ʌ^�Ƃ��ă��T�[�W���̊����ȉ��ɋL�ڂ���B
�����Ƃ��āA�}��ϐ��\���ɂ����ł���B���K�^�ɂ��\�L���m���Ă��邪�A���������Q�Ƃ̂��ƁB���S�ҁE��ʌ����̃��T�[�W���E�}��ϐ��\���㐔�̓��发������B
Y=a*tri(a*t-tc)+C
X=a*tri(a*t-tc)+C
tri() :�O�p���E�T�C�����̓R�T�C���ł���B
�@�ȉ��́A���T�[�W�����Q�̊g���Ƃ������ƂɂȂ�B�@����ɂ��Ă��A���炭�͖c��Ȍ������ʂ����݂��Ă��锤�ł���B�����m�̕��͈��������Ƃ��肪�����B
�P�j
Y=a*tri(a*t-tc)+C�{a*tri(a*t-tc)+C�{���i���j
X=a*tri(a*t-tc)+C�{a*tri(a*t-tc)+C�{���i���j
�����̋Z�@���l�ɁA�قȂ�����E�U���̊��������Ă����A�Ƃ����g���ł���B
�Q�j
Y=�ia*tri(a*t-tc)+C�j��a*tri(a*t-tc)+C�{���i���j
X=�ia*tri(a*t-tc)+C�j��a*tri(a*t-tc)+C�{���i���j
Ex.) 1.0
Ex.1.0
�̃v���O�������ȉ��Ɍf�ڂ���B
10
20 scale=100
30 t=0
40 tunit=0.01
50
60 *main
70 '1
80 x=0.1*cos(1.2*t)
90 y=0.2*sin(t)
100 '2
110 x=x+2*cos(t/12)
115 y=y+1.5*sin(t/7)
120 '3
130
140 line -(200+x*scale,
200+y*scale), 7
150 t=t+tunit
160 goto *main
170
�i�v���O�����̏I���j
(End of paragraph)
Updated:3/11/2005 12:58:33 AM JMT
<End of contents. >